数学Ⅰ 2次関数 復習 復習 解の公式を使う 過去問解説 大学入学共通テスト2 次関数 演習問題 14 (1) ( ) ( ) x m m m x mx m y x mx m 4 4 4 4 2 4 4 8 4 2 2 2 2 = = = よって,x=mで最小値 2 4 4 m m をとる。 ゆえに, 2 = 4 4 l m m (2) ( )4 1 2 4 4 = = mm l m m より, l>0 であるための必要十分条件は (mm) > 4 1 0 すなわち (mm) < 1 0 \第2学年 3 一次関数 知識・技能の習得を図る問題 年 組 号 氏名 練習問題① 次の(1),(2)の各問いに答えなさい。 (1) 下のアからオの中に,y が x の一次関数であるものがあります。 正しいものをすべて選

2次関数23 2次関数の決定 怜悧玲瓏 高校数学を天空から俯瞰する
2次関数問題 高校
2次関数問題 高校-求める2次関数は y = a( x 1 )2 q とおける。 これが,2点( 1 ,9),( 0 ,3)を通るので,代入して x 軸と2点( 1 ,0),( 4 ,0)数学Ⅰ 2次関数章末問題解答 §1 2次関数 2次関数章末問題解答ヒントと解説 1 解説 平行移動前の関数上の座標を (x,y), 移動後の点を (X,Y) とする。 すると (X,Y) は,X=x1,Y=y3 と表すことができる。 よって,x=X1,y=Y3 となる。 関連項目:1.点とグラフ




2次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する
MathAquarium練習問題2 次関数 2 2 (1) 放物線y=-2x2-14x-13 をどれだけ平行移動すると,放物線y=-2x2+8x+7 に重なるか。 (2) 2 次関数y=x2+ax+4 のグラフを,x 軸方向に2 だけ平行移動すると2 次関数y=x2-9x+b の グラフとなる。このとき,a,b の値を求めよ。 2次関数の決定 基本形 y=a (x−p)2q または 一般形y=ax2bxc として係数を求める。 軸や頂点に関しての条件が与えられた場合 基本形 を使い、 グラフ上の点が3点が与えられた場合は 一般形 を使うなど 条件に応じて都合の良い方を選ぶ。Y=x 2 2 (x≧0)の逆関数を求める問題ですね。 重要なのは, x≧0 という定義域です。 実は,2次関数は,このように定義域を設定しないと,逆関数を考えることができないのです。 1つのxの値に対し,yの値が2つ出てしまう
0403二次関数の平行、対称移動(難易度2) 19/3/18 19/3/21 問題 関数を y 軸に対称移動し、 x 軸に 2 、y軸に − 1 平行移動すると、 y = − x 2 2 x 3 の関数となった。 元の関数を求めよ ヒント 対称移動と平行移動したときの、変数の置き換えを使います 二次関数の最大値・最小値の問題 二次関数の最大値・最小値を求める問題では、「 頂点を調べること 」「 グラフを書くこと 」が最大のポイントです。 つまり,2次関数の最大,最小の問題は,頂点が定義域に含まれるかどうかで,さまざまなケースが考えられるのです。 最後に,2次関数と方程式,不等式の関係について学習します。2次方程式ax 2 bxc=0 の解の個数は,2次関数y=ax 2 bxc とx軸との共有点の個数に一致します。2次方程式の単元で
2次関数 中学3年生 数学 2次関数 練習問題プリント 無料ダウンロード・印刷 「1つの解が分かっていて、もう1つの解や係数を求める場合」「2つの解が分かっていて係数を求める場合」と、様々な文章題の解き方を練習できます。/1/7 2年一次関数総合問題Lv3 5(2) 点Pはlとx軸の交点(誤)→点Bはlとx軸の交点(正) 3年方程式文章題(割合2)3(1)解答 2番目の式 yの係数 97 100 (誤)→ 93 100 (正) 7 3年2乗に比例する関数総合問題4 5問題 点A, P, Qを頂点とする(誤)→点D, P, Qを頂点とする(正)2次方程式の活用(2) 2次方程式の活用(3) 4 関数 y 問題一括 (2,462Kb) 解答一括 (2,734Kb) 円周角と中心角(2) 円周角と中心角(3) 等しい弧と円周角 円周角と図形の証明 円周角の定理の逆 円周角の定理の活用 7 三平方の定理 三平方の定理の証明(1) 問題一括 (3,793Kb) 解答一括 (4,569Kb) 三平方の




数 2次関数 標準形の求め方 素早く頂点を求める手法の紹介 教えたい 人のための 数学講座




高校数学 Y A X P 2のグラフ2 例題編 映像授業のtry It トライイット
2次関数・2次関数のグラフ基本問題~高校数学問題集 2次関数・2次関数のグラフ基本問題~高校数学問題集 ※表示されない場合はリロードしてみてください。 (表示が不安定な場合があり,ご迷惑をおかけします) Download シェアする Twitter Facebook 0 はてブ 0 LINE naopを練習問題③ 4 次の(1)から(3)までの各問いに答えなさい。 (1) 次の一次関数のグラフをかきなさい。 ① y =x -2 x ② y =- x +2 x ③ y =-3x -6 x (2) (1)の3つの直線で囲まれた三角形の面積を求めなさい。ただし,面積の単位は考えな いものとします。上の問題1の(1)~(5)で1次関数はどれか。すべて答えよ。 y=3x12 について次の問に答えよ。 x=2のときのyの値を求めよ。 x=3のときのyの値を求めよ。 y=15のときのxの値を求めよ。 y=2x6 について x=2のときのyの値を求めよ。 x=5のときのyの値を求めよ。
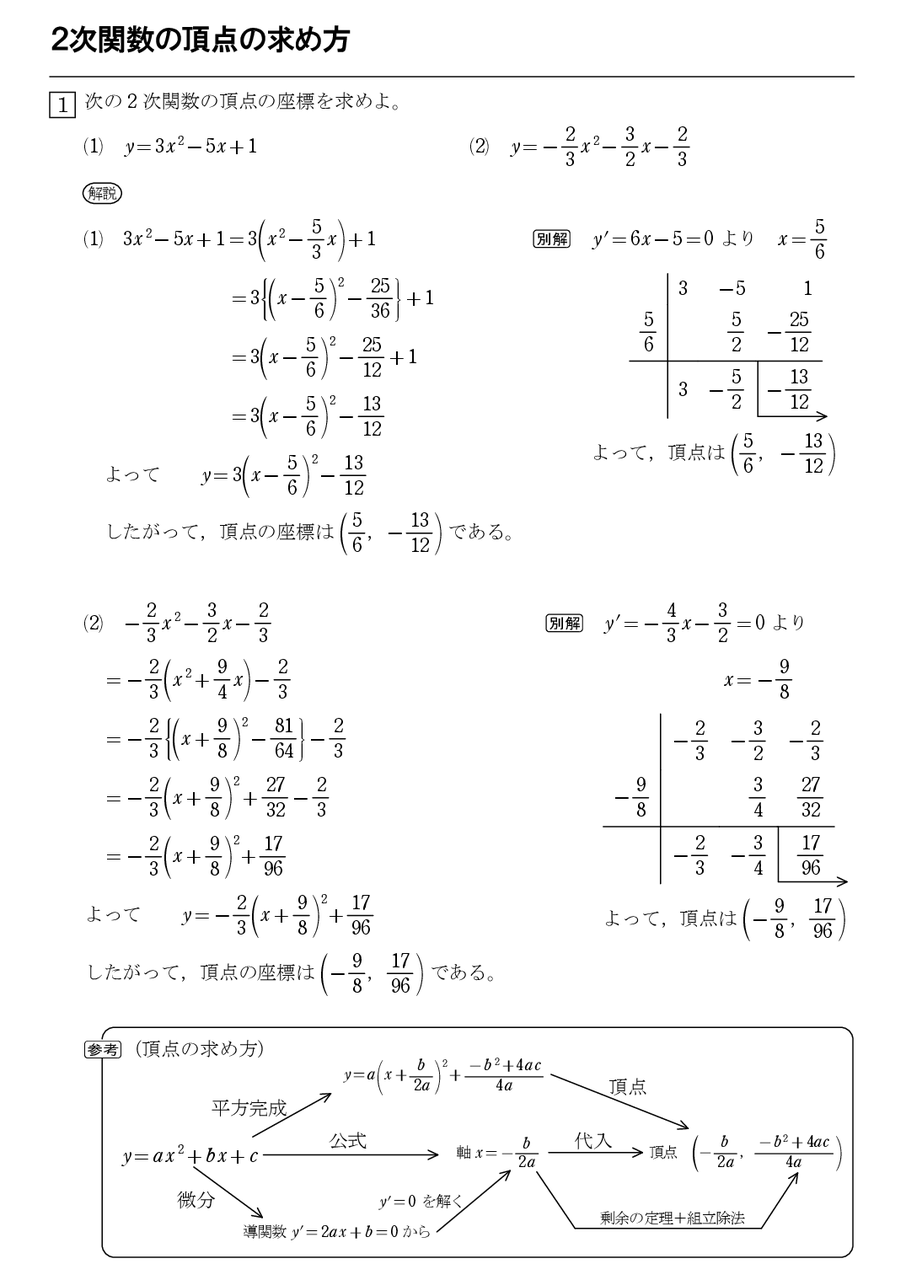



2次関数の頂点を求める別解 怜悧玲瓏 高校数学を天空から俯瞰する




数学1 2次関数勉強法 センター数学頻出の2次関数をマスターするポイント
2次関数の平行移動を使った問題 y=ax²のグラフを 平行移動 して、 ・ "y=a (xp)²" ・ "y=ax²+q" ・ "y=a (xp)²q" の形にすることはすでに学習済みかと思います。 ここでは、これらの平行移動のテクニックを使った練習問題を一緒に解いて、理解を深めて 今回の問題はこちら。 k を定数とし、2次関数 y = x 2 − 2 k x 2 k 3 のグラフを C とする。 C が次の条件を満たすように、 k の範囲を求めよ。 問1: x 軸と異なる2点で交わる。 ここでは2次関数に関する応用問題を解説します。 様々な問題を解くことによって,それぞれの問題の考え方を身に付けましょう。 Contents 1 2変数関数の最小値を求める問題;




大学入試共通テスト数学の裏技 2次関数の最大 最小は 頂点と区間の端を調べよ 受験の月
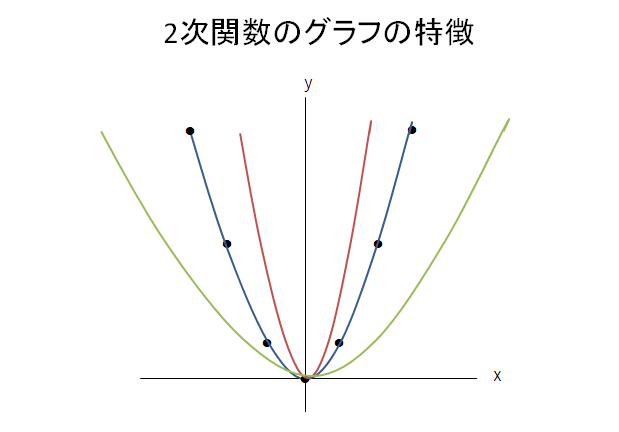



中3数学 二次関数のグラフの要点まとめノート 中学生勉強サイトあかね先生
2次方程式が出てくる,中3の5月~7月ごろに丁度良い問題。 ・反比例と格子点(★★★☆☆)(16年度大阪府) 1回経験しておくと良いかも? ・1次関数総まとめ問題(★★★☆☆)(21年度秋田県) 非常に無難な問題。 ・関数平行移動と無理やりな教育的・新共通テスト意識問題とgrapesの使い方(21年宮城県) 今回は変化の割合について見ていく。 公立入試で出題された場合、正答率が40%~60%程になっているようだ。公式や、やり方を忘れやすいのだろう。入試直前に復習しておくことを推奨する。 次回 2次関数の文章題①(制動距離・平均の速さ) 前回 2次関数と変域(基~標)2次関数(放物線)の移動は,頂点の移動で捉えられる. 問題2 1 2次関数 y=−x 2 2x3 のグラフを原点に関して対称に移動し,さらに x 軸方向に a , y 軸方向に b 平行移動すると頂点の座標が (1, 1) となった.このとき a= セ , b= ソ である. (玉川大14年度) 解説 やり直す a=2, b=3 a=2, b=5 a=4, b=3 a=4, b=5 y=−x 2 2x3=− (x 2 −2x)3 =− { (x−1) 2 −1 } 3




高校 数学i 二次関数とグラフの問題です Clear



数学 二次関数グラフの書き方を初めから解説 Youtube
「 2次関数 」カテゴリーアーカイブ 投稿ナビゲーション ← 過去の投稿 年 大阪学院大 投稿日時 21年5月8日 投稿者 tkame 返信 上の問題文をクリックしてみて下さい. リンク:1次方程式 (3)は左辺と右辺の関数のグラフを考えましょう. カテゴリー 数学I, 2次関数 タグ 1次方程式, 1次2次関数のセンター試験問題 → 携帯版は別頁 センター試験問題 2次関数 センター試験 06年度:数学I・A(本試験) 第2問 2次関数 y=6x 2 11x−10 ① について考える. ①において, y≦0 となる x の値の範囲は2次関数の問題 Try IT(トライイット)の2次関数の様々な問題を解説した映像授業一覧ページです。 2次関数を探している人や問題の解き方がわからない人は、単元を選んで問題と解説の映像授業をご覧




高校数学 2次関数がx軸から切り取る線分の長さ 受験の月
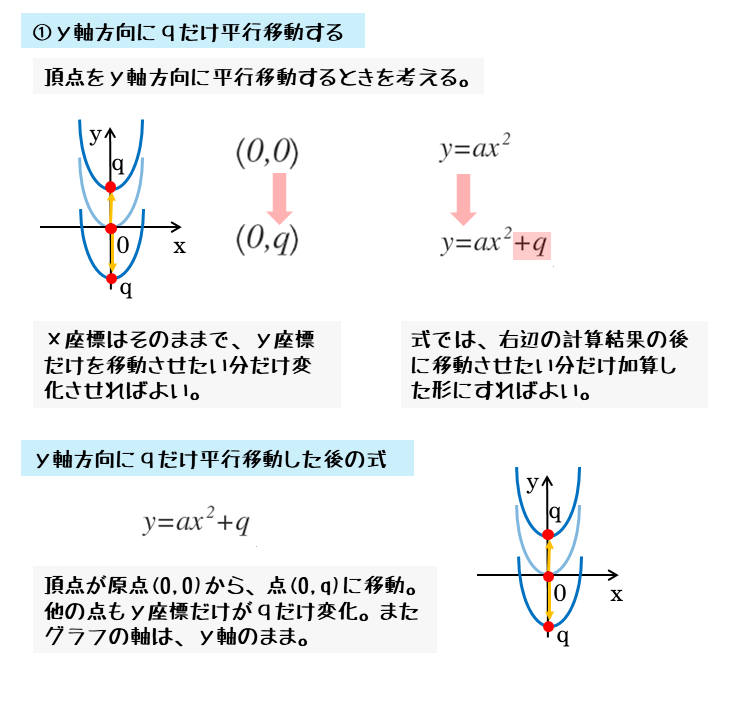



2次関数 2次関数のグラフの平行移動について 日々是鍛錬 ひびこれたんれん
計画問題という.2次計画問題の目的関数が凸関数である場合について,その問題 の最適解であるための必要十分条件を解説する.また,双対問題を導入し,線形計画 問題の場合と同じように,弱双対定理と双対定理が成り立つことを示す.そして,凸 2次計画問題を解く主双対内点法のパス2次方程式の整数解問題 実践例題③1 例題3 解答 2次方程式x2 (a1)x3a 1= 0 が整数解を少なくとも1つもつとき, 整数 a の値を求めよ。 2次方程式の整数解問題は,まずは,判別式 D≧0 より,範囲が絞れないか試してみるが,この場合 絞れない。そこで,文字(整数)にMathAquarium練習問題+解答2 次関数 1 2次関数 1 (1) 2 次関数y=-3x2-2x+1 の頂点と軸と求めよ。また,グラフをかけ。 (2) 2 つの放物線y=x2-8x とy= x ax 3b 2 - 1 2+ - の頂点が一致するときのa,b の値を求めよ。 解答 (1) y=-3x2-2x+1= 1 3 2



48s96ub7b0z5f Net Nijikansu Graph




センター試験09年度数学1a第2問 二次関数の最大値 最小値の問題の解説 受験数学かずスクール
高校数学の要点, 無料の練習問題, 例題と解説 2次関数の最大と最小2次関数と1次関数の融合問題(放物線と直線)のポイントは! y=ax^2 の a の値は、通る点が1個わかれば求まる!🎥関連動画🎥 1次関数の式の求め2次関数1 応用学習 グラフで迷わず場合わけ 練習問題 今回は ・2 次関数の最大・最小 ・2 次関数の最大・最小(文字定数をふくむ) について学習しました。学習内容をまとめておきますので,問題を解く前に確認しておきま しょう。 2 次関数の最大・最小 1 2 次関数の最大・最小 関数の値域
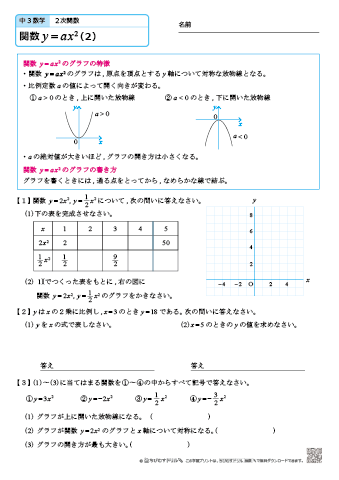



中学3年生 数学 2次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく
今回は、2次関数の問題を解く上でどのように指数対数や三角関数などの問題を解くのに役立つか何問かの問題を通して理解していってもらいたいと思います。 基本的なことから解説しているので、数学が苦手だという人に読んでほしいです。 2次関数と指数対数、三角関数の関連性その1 2次 数Ⅰの最重要単元、2次関数の特訓プリントです(`・ω・´) 文字を多く扱う単元ですが、しっかり考え、手を動かして、式やグラフを描きながら解いていきましょう! 平方完成 数学Ⅰ 2次関数 平方完成特訓① (文字を含まない2次関数) 問題編 数学Ⅰ 2次関数 平方完成特訓① (文字を含まない2次関数) 解答編 平行移動・対称移動 数学Ⅰ 2次関数 平行移動・対称2次関数の定義域が 0≦x≦a 2次関数の最大最小値の問題で、定義域が変数で与えられている場合があります。 y=x²−4x+5 においてxの定義域が 0≦x≦aのときの最大値を求めなさい。 このような問題です。 一緒に解きながら説




2次関数の練習問題 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc




Amazon Fr 大学入試 苦手対策 2次関数 三角関数 指数 対数関数 に強くなる問題集 Livres
1次関数の問題(2) プリント用PDF:一次関数の問題(2) 1下の図のような長方形ABCDで,点PはAを出発して,返上をB,Cを通ってDまで動く。辺AB=6cm,辺BCを12cm,点PがAから $ x $ cm 動いた時の APDを $ y $ ㎠ として下の問いに答えなさい。 (1)点Pが辺AB上にあるとき,辺BC上にあるとき,辺CD上にある次の問いに答えよ。 y=3x12 について x が 7 増加するときの y の増加量を求めよ。 x の変域が 1≦x≦3 のときの y の変域を求めよ。 6x3y11=0 の傾きと切片をそれぞれ求めよ。 次の中から y=5x12 と平行なものをすべて選びなさい。 ア)y=2x12 イ) y=5x12 ウ) y=−5x 2 3 エ) 5xy8=0 オ)15x3y1=0 次の直線の式の中から ア)x 軸に平行、 イ)y 軸に平行 となるものを2年 連立方程式 解と係数 (1)問題, (3)答b=5 (誤) b=3 (正) 1年 文字式の計算2 (加減)3③答 17 a → − 17 a 2年 角度2 3③130°→131° 3年 放物線と図形1 5 (3)解答 (0,4)→ (0,4)または (0,4) 1年 文字式の計算3 (乗除) 答3③9c誤→49c正 1年 文章を等式にする 答 (9)12x→ 9 2



数学i Aチェック リピート 第2章 2最大 最小 2 2次関数の最大 最小 Pukiwiki




バカでもわかる 中学数学 2次関数
関数の文章題を解くときの最重要ポイントは、 「y=(xの式)」 を作ることだよ。 文章から式を作ることができれば、あとはいつもの関数の問題と同じになるんだ。 「y=(x 2 の式)」 がでたら2次関数問題閲覧 今は公開中 12次関数と解の配置 《千葉大12年》 問題を見る 公開中 22次関数の最大最小 《慶応大経済学部14年》 問題を見る 公開中 3解の配置と最大最小 《京都大05年》 問題を見る 公開中 42次関数と領域 《東北大11年》 問題を見る 公開中 5実数条件 《一橋大01年




高校数学 数 50 2次関数の決定 Youtube
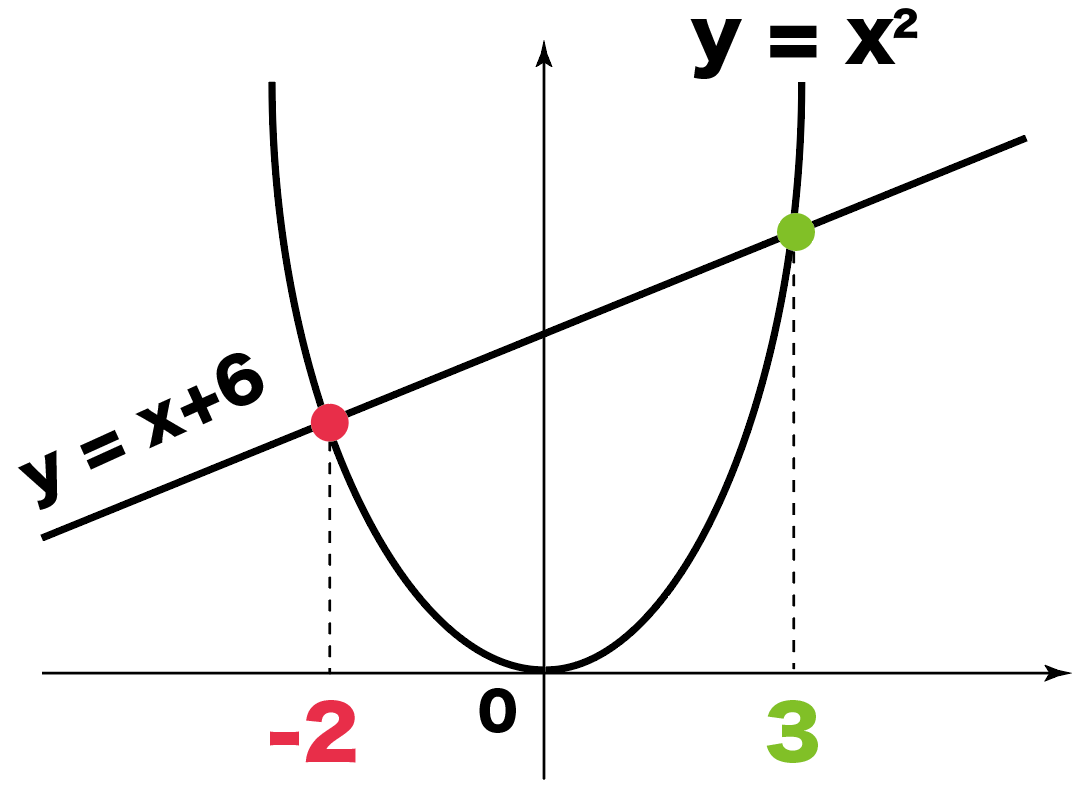



一次関数と二次関数の交点の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




数 2次関数 対称移動 1つの知識から広く深まる世界 教えたい 人のための 数学講座




世界一わかりやすい数学問題集中3 4章 二次関数




中学2年生 数学 1次関数 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




二次関数 場合分け チーム エン




二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局
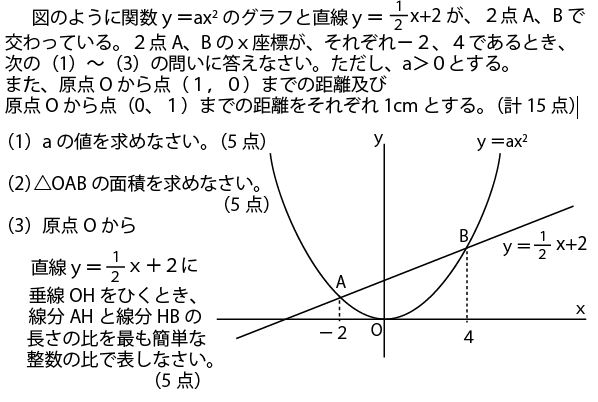



17年前期 千葉県公立高校入試数学 第3問 二次関数 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
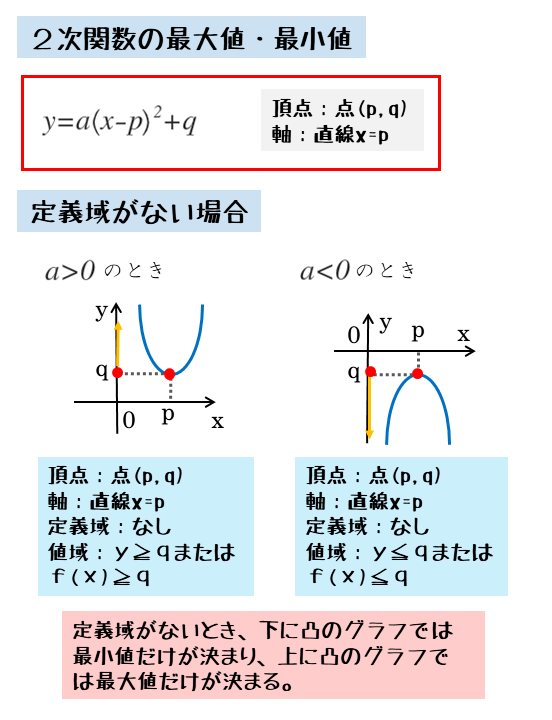



2次関数 2次関数の最大値や最小値について 日々是鍛錬 ひびこれたんれん




2017年 東大理系数学 第5問の解説 二次関数 二次曲線 放物線 接線 判別式 オンライン受講 東大に 完全 特化 東大合格 敬天塾




高校数学 軸に文字を含む場合の最大 最小1 例題編 映像授業のtry It トライイット




二次関数のグラフと問題の解き方 覚えておくべき2つの公式




2次関数23 2次関数の決定 怜悧玲瓏 高校数学を天空から俯瞰する




2次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する



二次関数の利用 グラフ系の問題 苦手な数学を簡単に




二 次 関数 数学入門 二次関数をシミュレーション 図解で理解 Amp Petmd Com




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




高校1年の二次関数 最大値 最小値を求める問題です Clear



改訂版 クリアー数学 P47 15 2次関数の最大 最小



中学3年生 数学 2次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学数学問題集 中3 2次関数 18 4 中学数学高校数学個別指導in山形市 数専ゼミ



2次関数問題 Of 京極一樹の数学塾会員頁




数 2次関数 関数の決定その1 頂点と軸が分かる場合 平行移動と媒介変数がポイント 教えたい 人のための 数学講座



2次関数 京極一樹の数学塾




2次関数 放物線 と1次関数 直線 の交点に関する問題のポイント 解説 数学fun




Luatexで2次関数の頂点を計算する問題の解答を作る 2次の係数は1 頂点整数のケース Baruku07のブログ
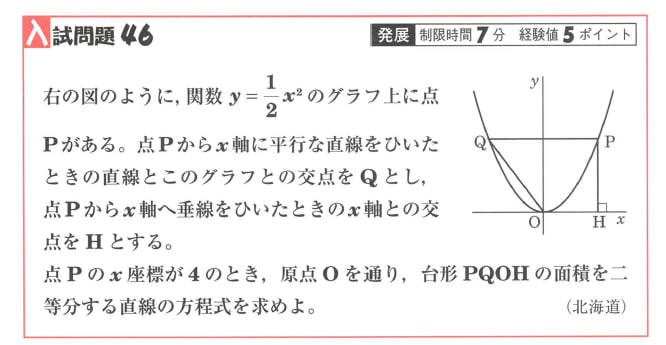



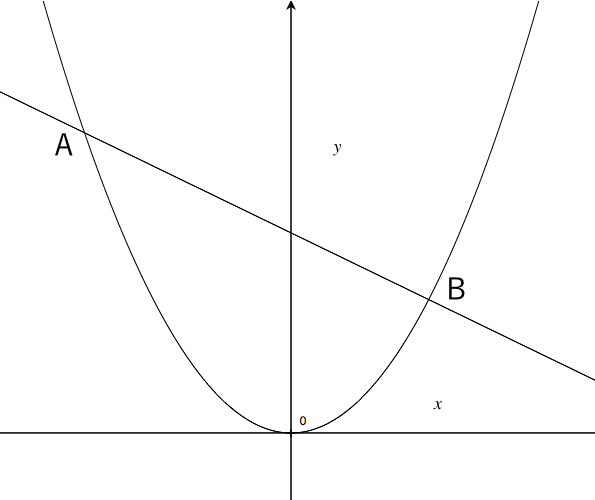
中学数学 1次関数 2次関数 46 北海道 宮城県 高校入試問題 英語 数学 さくら教育研究所 中学 高校受験 Skredu




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




数学 中3 41 二次関数の利用 一次関数とのコラボ編 Youtube



二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局



2次関数 2次方程式の解の存在範囲と判別式 数学 定期テスト対策サイト




中学3年生 数学 2次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
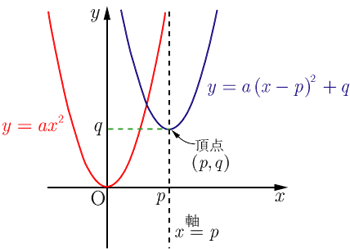



2次関数のグラフ Y A X 2 P Q




高校数学 2次関数の文章題 例題編 映像授業のtry It トライイット




数学 中3 42 二次関数の利用 一次関数との交点編 Youtube
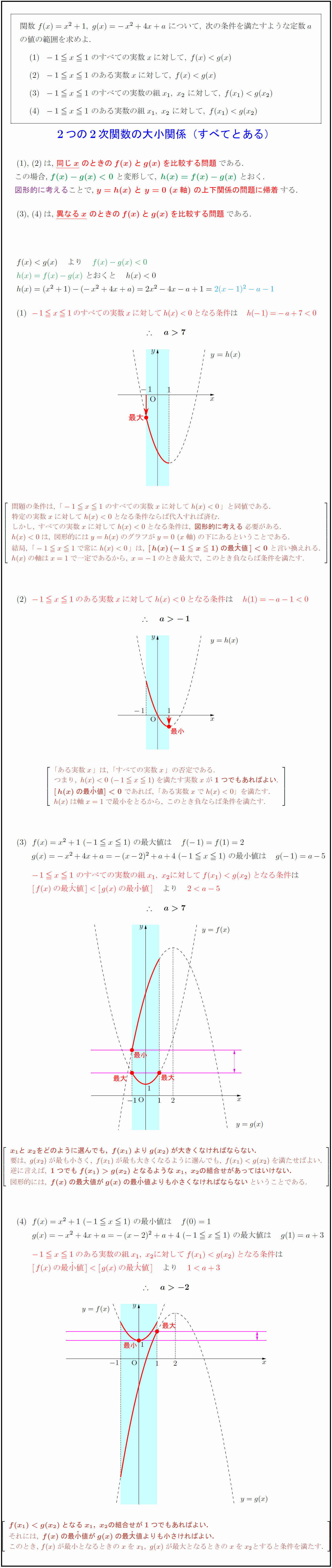



高校数学 2つの2次関数の大小関係4パターン すべて と ある 受験の月



二次関数の移動
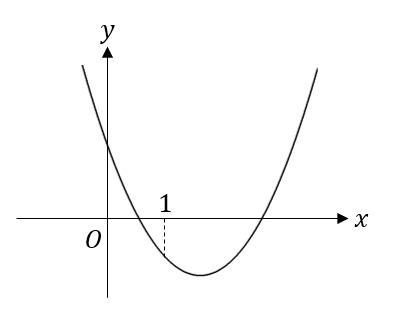



二次関数 係数の符号の決定 グラフから符号を決めるポイントを解説 数スタ
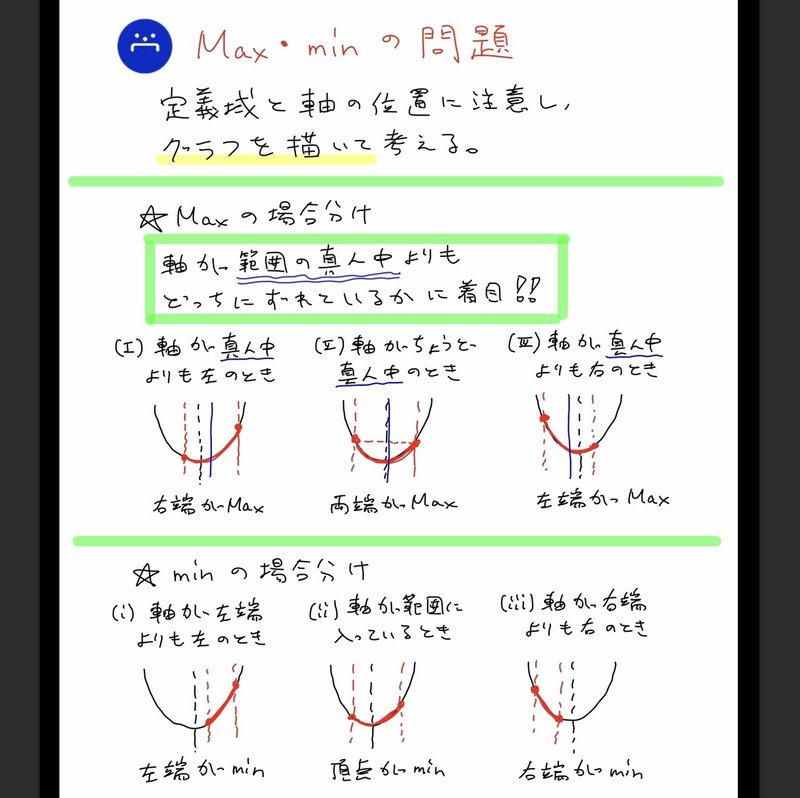



高校数学無料問題集 数 第2章 2次関数 最大値と最小値 桝 ます Note




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ
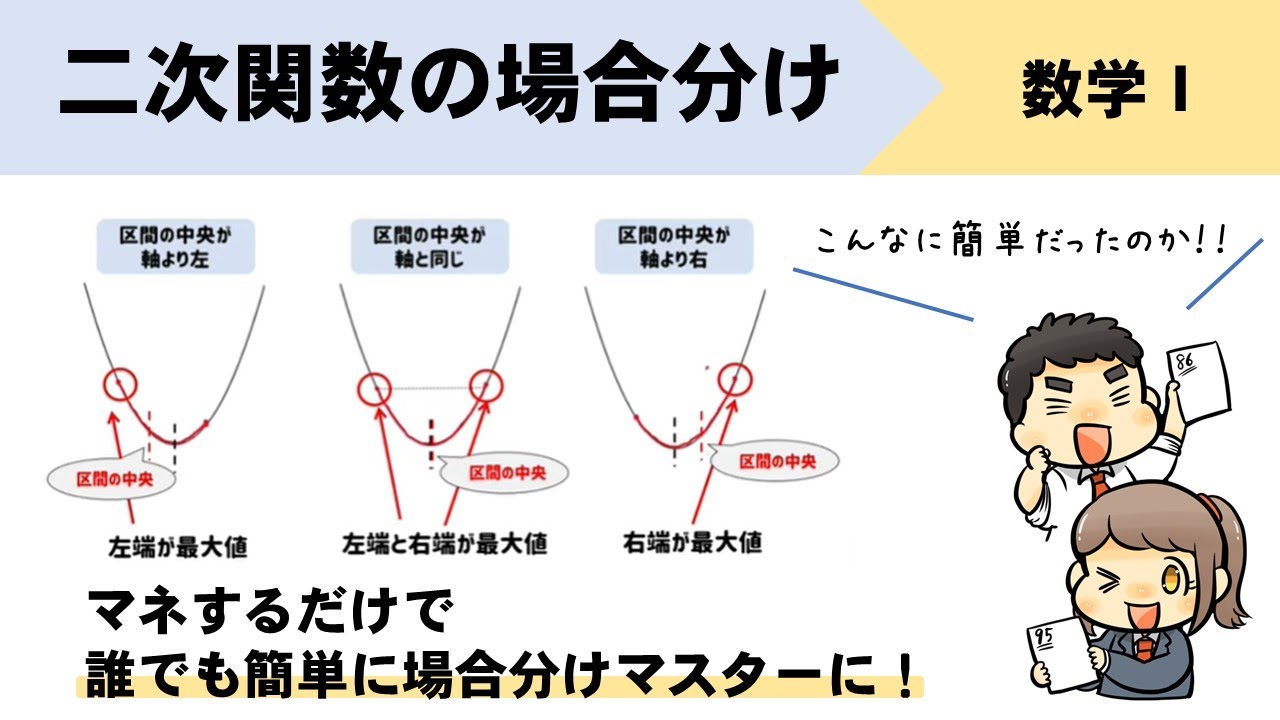



二次関数の場合分け 最大最小の応用問題の解き方をイチから解説 Youtube



2



ほのぼの数学頑張ろう 2次関数の最大 最小の問題 その3



二次関数とは 平方完成の公式や最大値 最小値 決定の問題 受験辞典
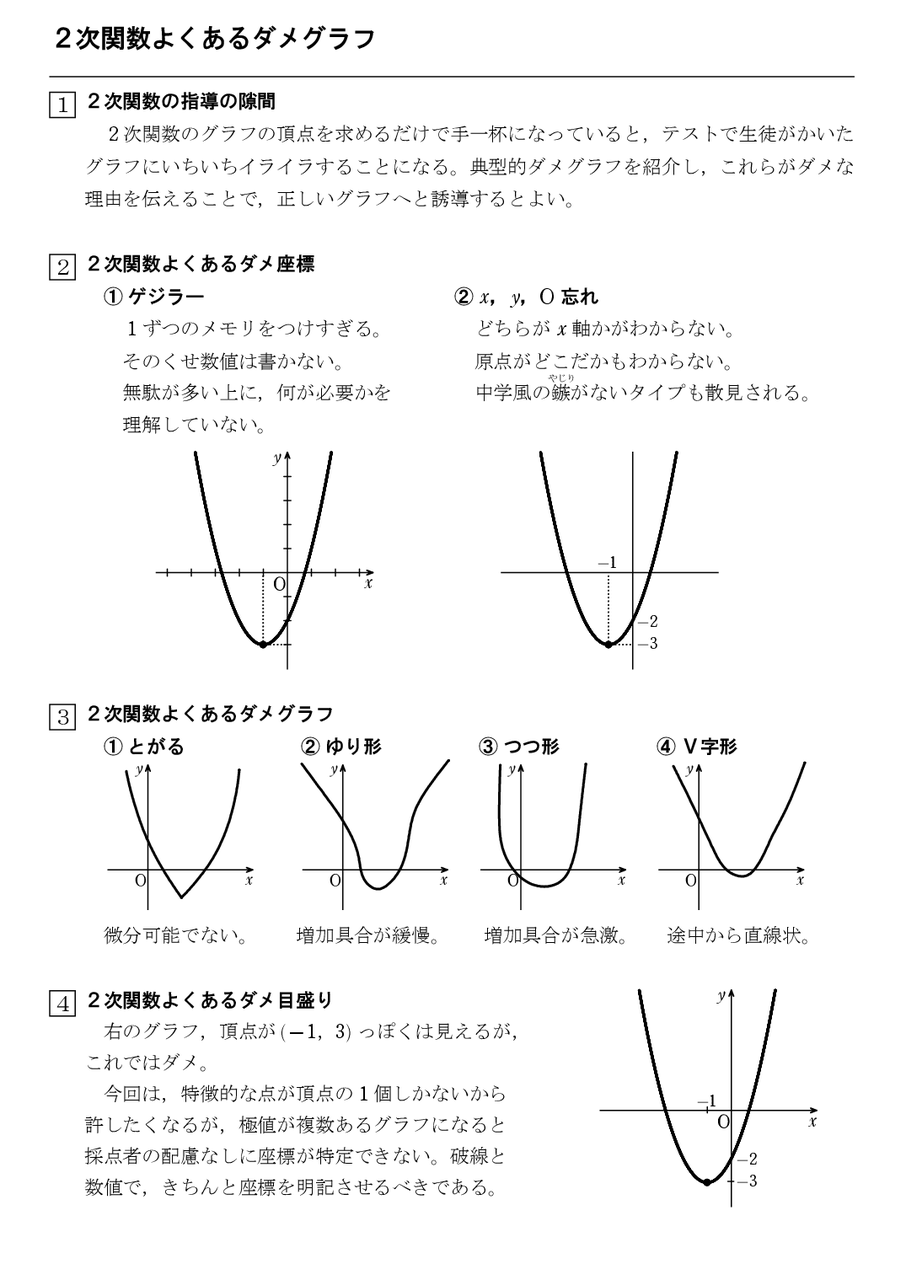



2次関数の最大最小問題にグラフは必要か 怜悧玲瓏 高校数学を天空から俯瞰する




数学 A 2次関数 Basic 理系ラボ




これで点が取れる 単元末テスト 中3数学 4章 二次関数




2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張



中学生がつまずきやすい数学分野




2次関数 媒介変数 スタディーx




数学 中3 35 二次関数のグラフ Youtube




数1二次関数です 1 についての質問です Clear
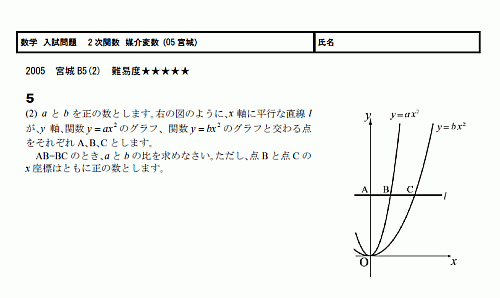



2次関数 媒介変数 スタディーx



1



1




世界一わかりやすい数学問題集中3 4章 二次関数
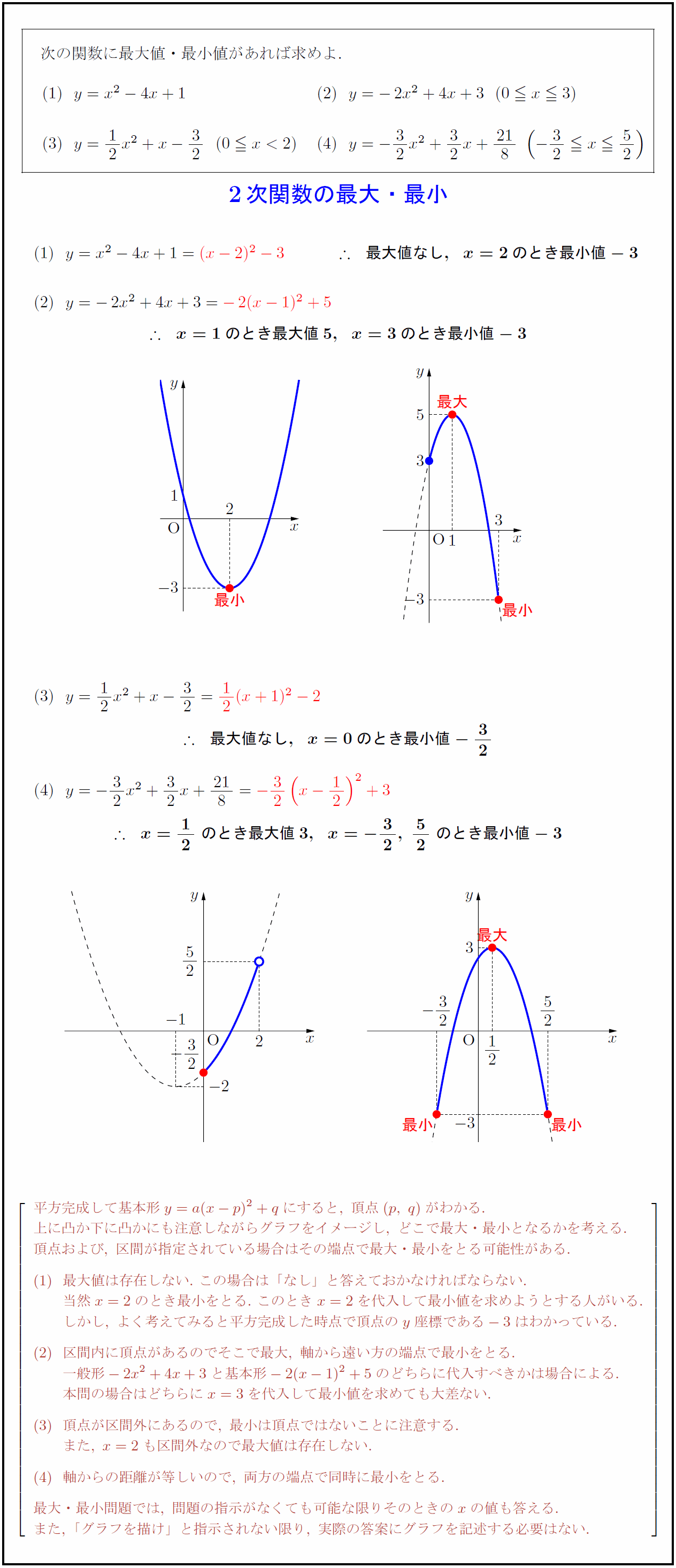



高校数学 2次関数の最大 最小の基本 受験の月




数 2次関数 最大値と最小値 基本編 基本はグラフ そして 教えたい 人のための 数学講座
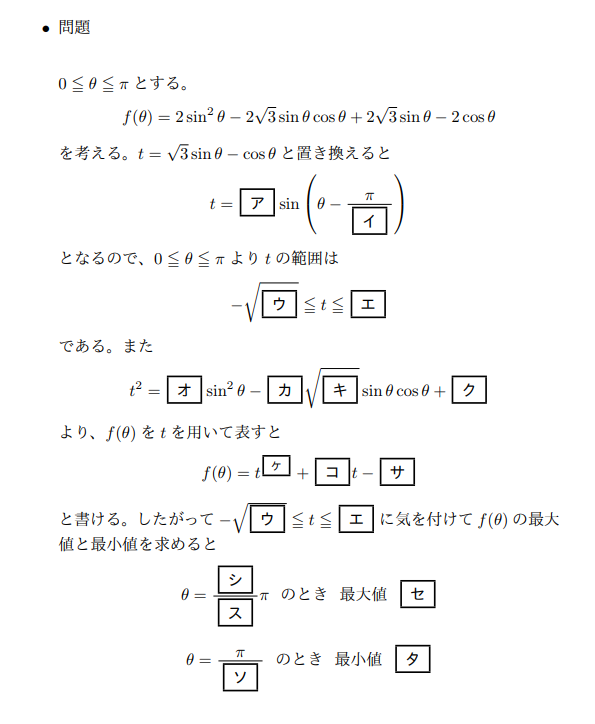



三角関数講座その3 置き換え 2次関数 高校数学の知識庫
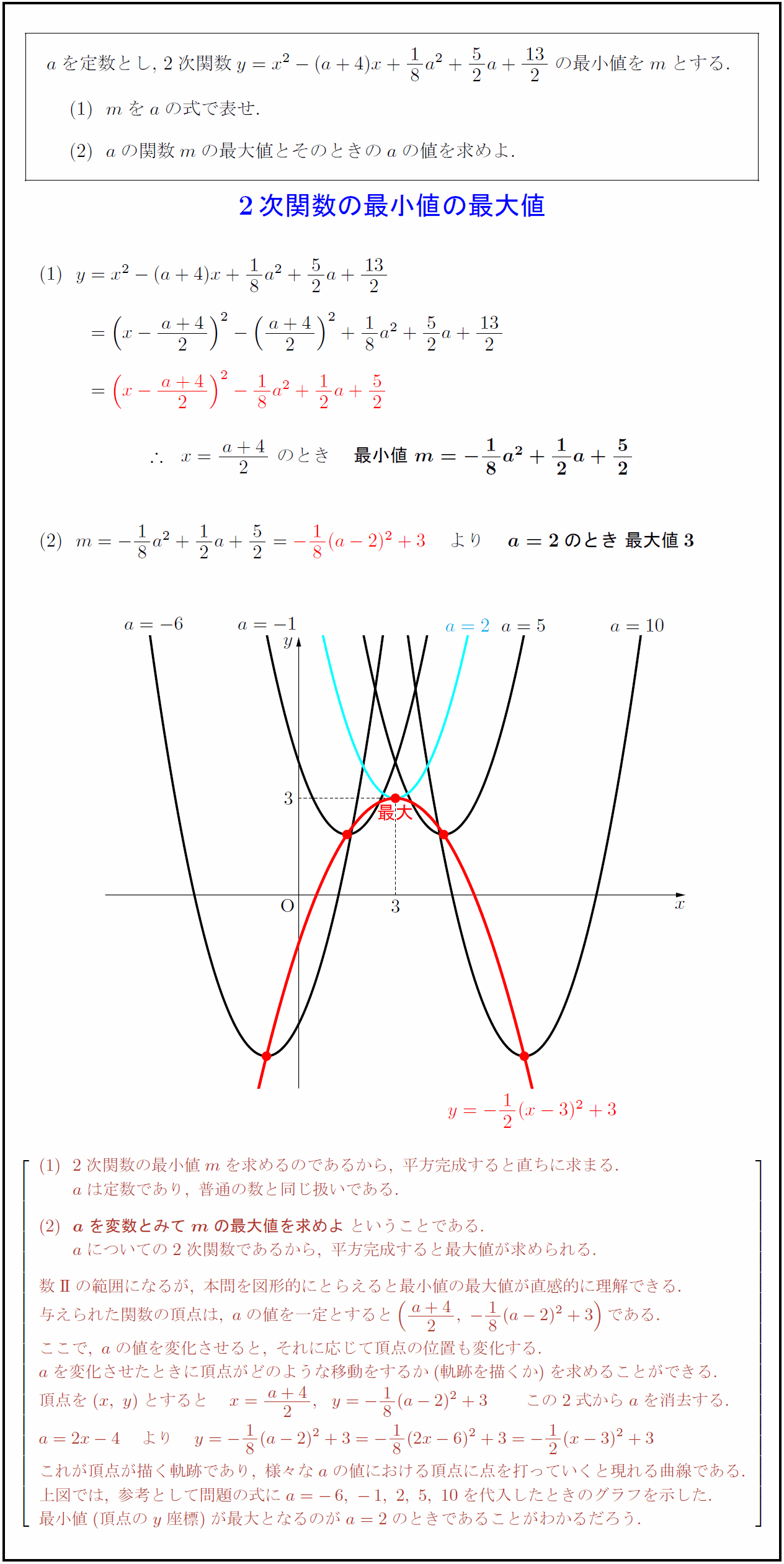



高校数学 文字を含む2次関数の最小値の最大値 受験の月




高校数学 数 37 2次関数 軸と頂点編 Youtube



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師




教科書レベルの問題一覧と解答 数学 2次関数 教科書より詳しい高校数学




数 2次関数 関数の決定その1 頂点と軸が分かる場合 平行移動と媒介変数がポイント 教えたい 人のための 数学講座




数 2次関数 関数の平行移動 操作は簡単 意味は深い 教えたい 人のための 数学講座



二次関数のグラフの書き方と公式を使った最大値最小値問題の解き方 Studyplus スタディプラス
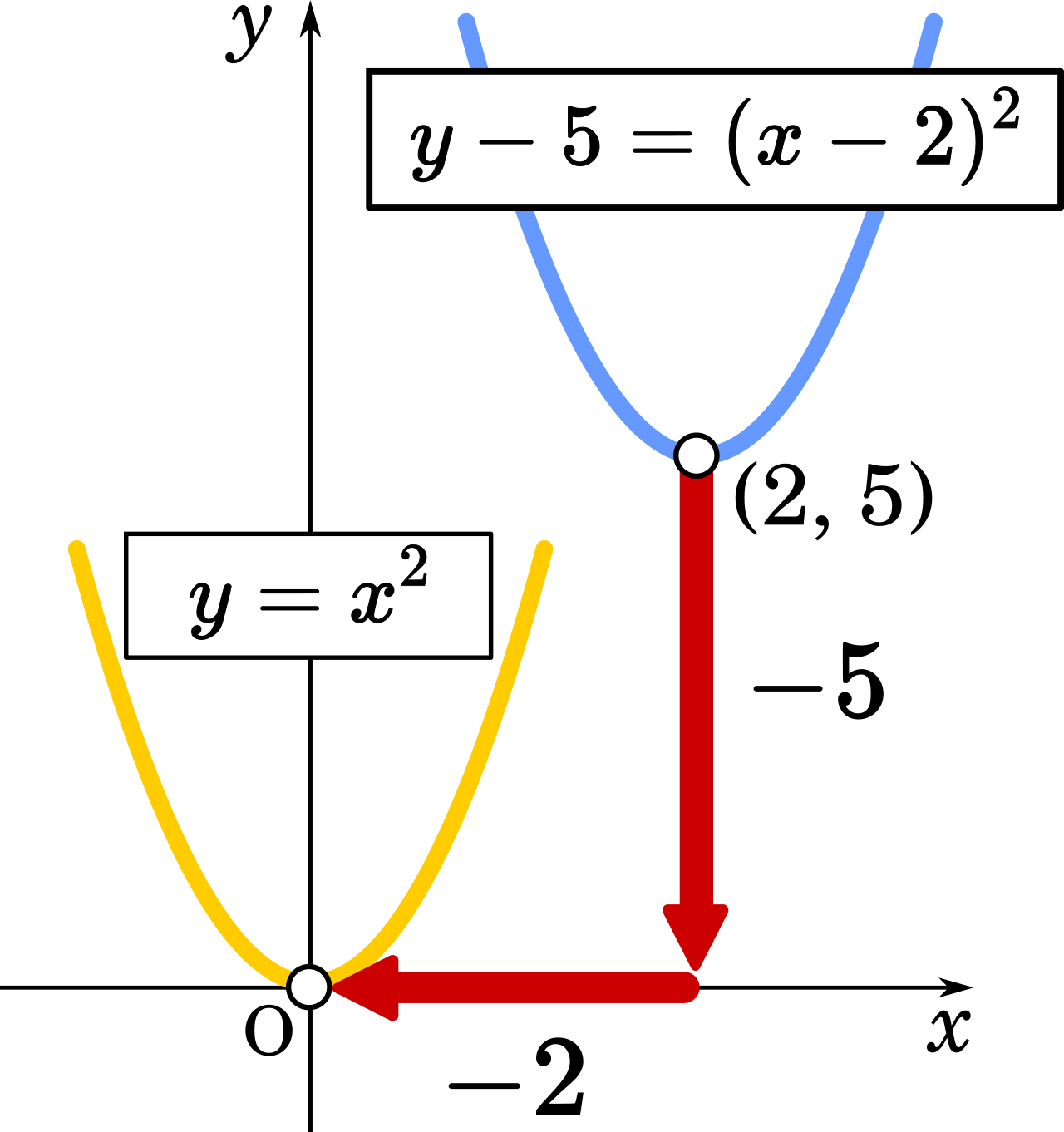



数 二次関数 平行移動の符号はなぜ反対になるのか 答えは見方が逆だから Mm参考書



1



1



48s96ub7b0z5f Net Nijikansu Heikoido




中学数学の二次関数 問題の解き方の基本とグラフの書き方 リョースケ大学




2次関数の問題に対する条件反射 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc



2次関数 京極一樹の数学塾




高校数学 数 49 2次関数の決定 Youtube




高校数学 2次関数のグラフy Ax Bx Cの係数の符号 受験の月




2次関数 2次関数の決定について 日々是鍛錬 ひびこれたんれん




超簡単 二次不等式の解き方が誰でもわかる 必ず解きたい問題付き 高校生向け受験応援メディア 受験のミカタ
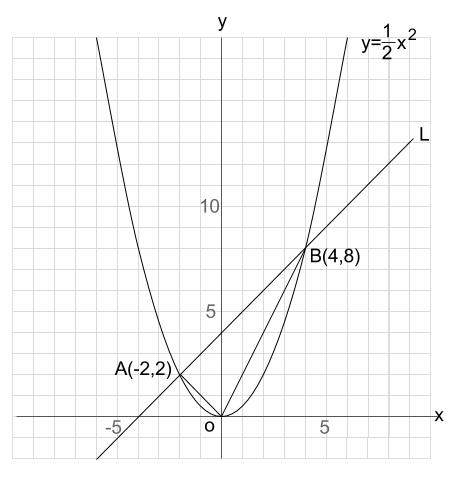



中学数学 Y Ax 2 図形との融合問題 中学数学の無料オンライン学習サイトchu Su




10 6 2次関数 動点 勉強できようサイト




2次方程式の解の配置問題 おいしい数学
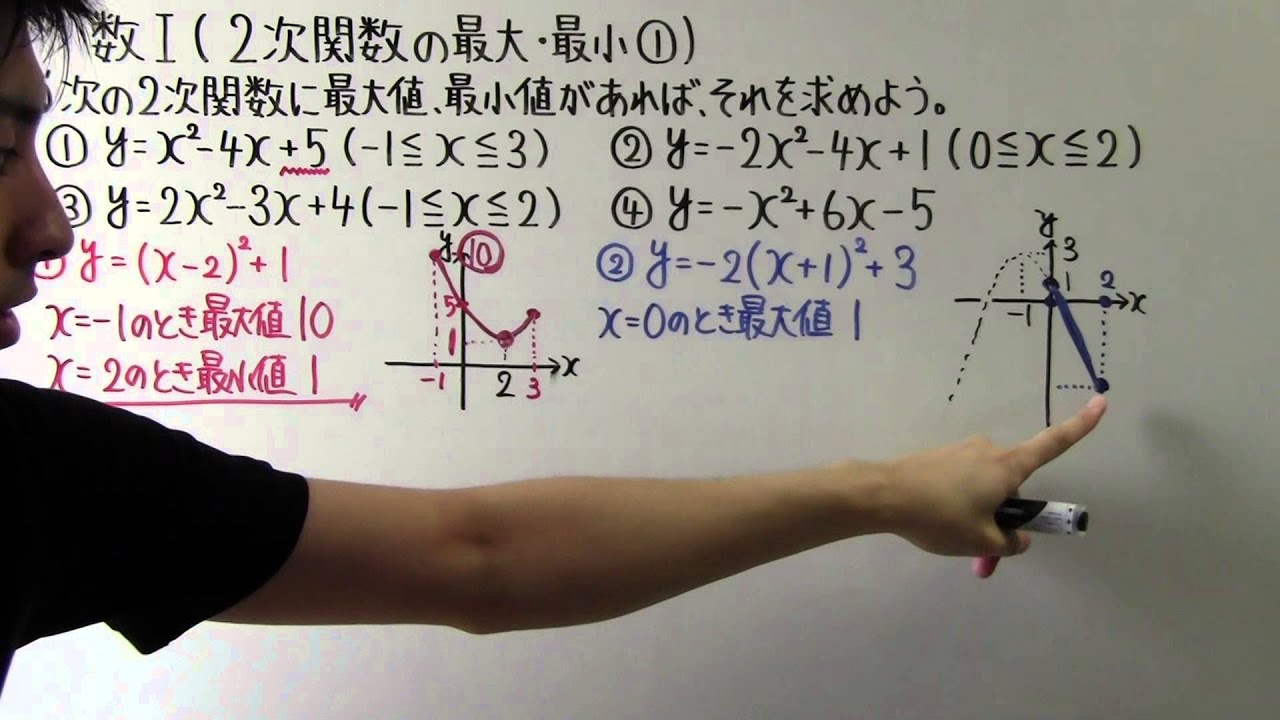



高校数学 数 42 2次関数の最大 最小 Youtube




高校数学 文字を含む2次関数の最大 最小 区間固定で関数の軸が動く 高校数学最重要問題 受験の月
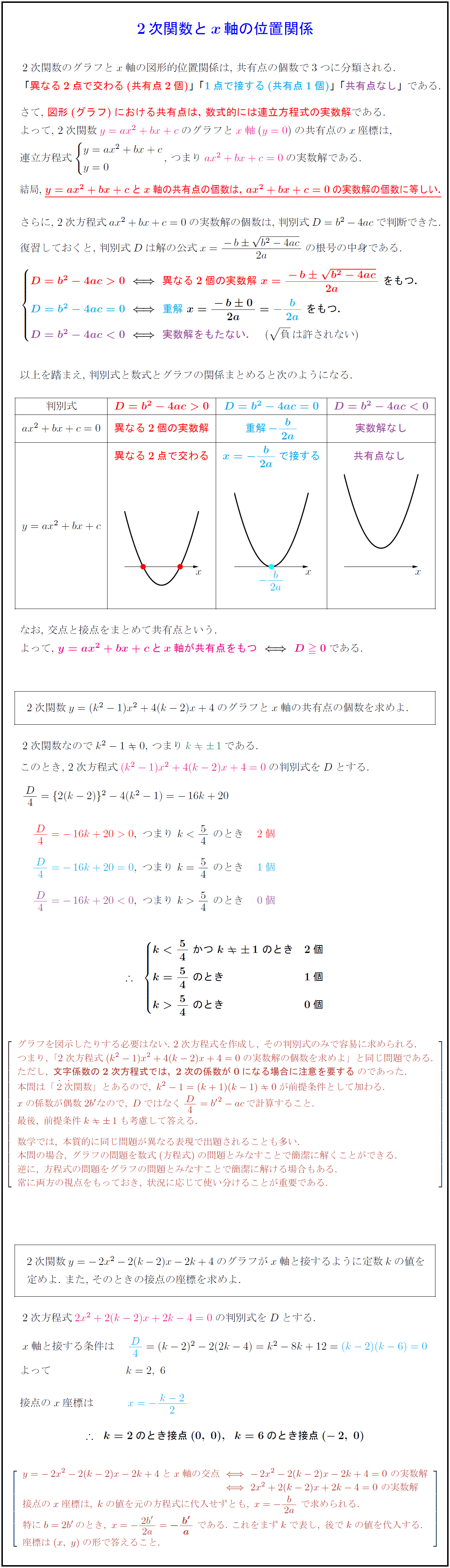



高校数学 2次関数とx軸の位置関係 共有点の個数 判別式d 受験の月




高校数学 数 35 2次関数 Youtube
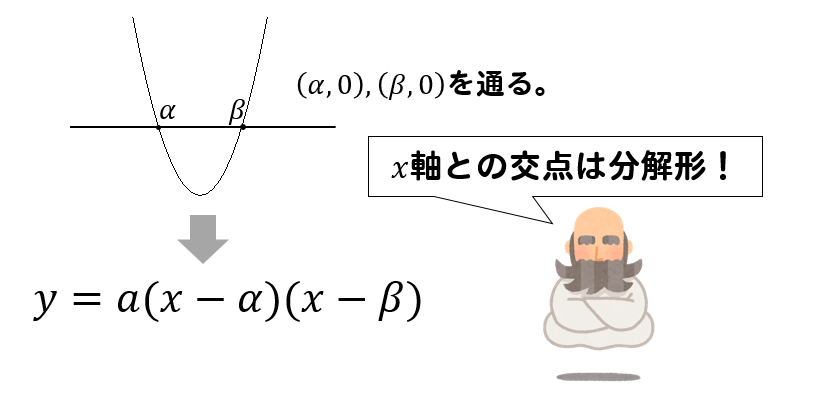



二次関数の決定 式の求め方をパターン別に解説 数スタ


